A Stack of Weights on the Descending Side

I won't be doing anything with this blog over the Easter holidays, so I'll make a couple of posts now.

Here is a screenshot of one of the earliest silux models I made. (I re-created it for this blog.)

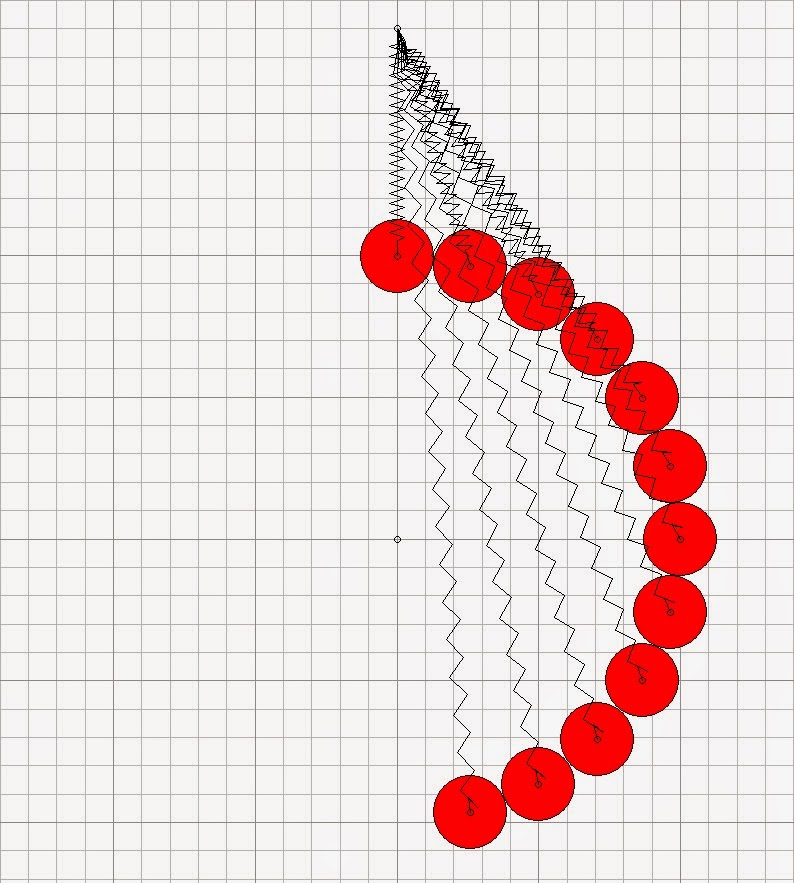A stack of weights, all on the descending side

Description

Each 4kg weight in the stack is attached to, and can pivot around the central fixpoint. (In my earliest models I used arms between the weights and the fixpoint, which may look more realistic, but are unneccessary in the model. I haven't bothered with them here). The weights also have tension springs to the upper fixpoint. As each weight falls, its spring is extended, storing energy. The lowest weight goes "over-center" and is then pulled up by its spring on the ascending side.

All weights except the bottom one should be pinned together, because even though the top weight is in unstable equilibrium, it doesn't move from rest in the model, if it is left isolated from the other weights.

Results

Does the lowest weight get back to top center again? Fairly obviously, no. Even though a model like this could have only one weight at a time on its ascending side, as opposed to any number of weights on its descending side, energy is always just conserved overall between potential energy and kinetic energy of the weights, and stored energy in the springs. What is more, and what is perhaps not always appreciated, is that in any device like this, energy is always conserved overall at every instant over the entire operating cycle.

Variations

I investigated a few variations of this model, e.g. with the upper ends of the springs no longer attached to a fixpoint, but attached instead to small-diameter rollers which themselves formed a vertical stack, being pulled downwards at an appropriate rate, and hence delivering energy into the system. But none of these variations gave any net energy output.